12月初，全国医保个人账户跨省共济工作启动，医保个人账户打破地域限制，职工医保个人账户将可以跨省用于本人近亲属缴纳居民医保和报销医疗费用，目前已在河北、江苏、安徽、山东、河南、湖北、重庆、四川、甘肃部分地区正式试点运行，其他省份和地区将会陆续开通，什么是医保个人家庭账户共济我国职工医保制度实行社会统筹和个人账户相结合的保障模式，职工医...。

据了解，一项代号为，布罗莫项目，的卫星合并计划目前正在讨论中，三方有意将各自的卫星资产合并重组为一家新企业，知情人士透露，成立合资公司可能需要数年时间，该计划仍处于初期阶段，目前尚不清楚合并后的新企业将如何运营，也不清楚是否会涉及任何人员裁员，知>，...。

导言纳维尔，斯托克斯方程是流体力学中的一个关键方程，它描述了粘性流体的运动，理解这个方程对于理解各种流体现象，如湍流和边界层，至关重要，本文将介绍如何使用张量语言来简化纳维尔，斯托克斯方程的理解，并探讨其与牛顿运动定律之间的联系，矢量微积分和张量语言传统的流体力学使用矢量微积分来对流体运动进行描述，张量语言提供了一种更简洁和通用的方法...。

前言在前两期直播课中，我们使用微分几何的语言计算了斯托克斯力，并得出了斯托克斯力的形式，整个过程中仍留有一个悬念，即从微分几何的角度理解应力张量，本期直播课将彻底解决这一疑惑，回顾，非直角坐标系中的微分几何我们回顾了使用微分几何求解非直角坐标系问题的便利性，具体来说，单位基矢，球坐标系中，单位基矢表示为，```e，r=∂r，∂re，θ...。

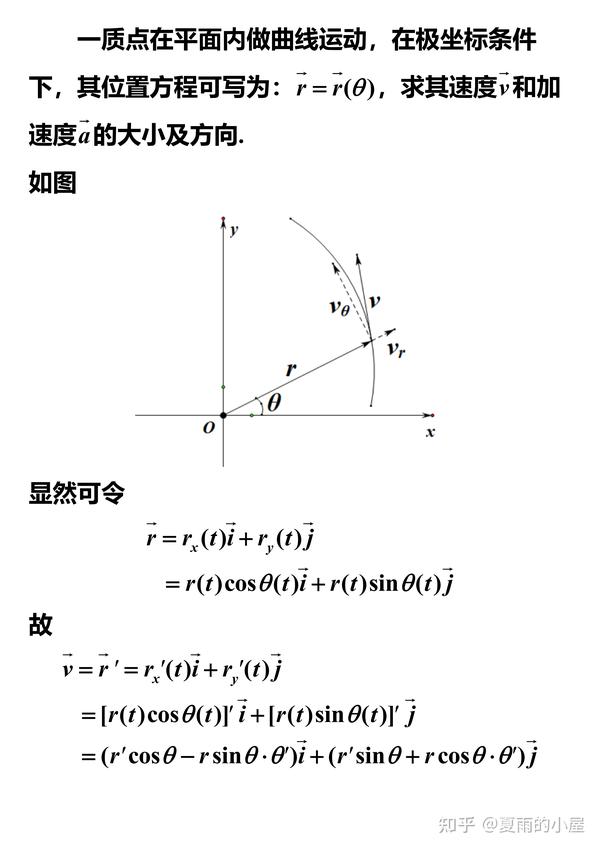
课程回顾在上两节直播课中，张朝阳教授用微分几何的语言计算了斯托克斯力，并得到了斯托克斯力的形式，但在整个过程中，仍然留有一个悬念，即从微分几何理解应力张量，单位基矢和坐标基矢按照上一节直播课的数学符号精神，在球坐标系下，单位基矢表示为，e，r=，sin，phi，cos，theta，sin，phi，sin，theta，cos，phi...。

回顾上一节直播课中，张朝阳用微分几何的语言计算了斯托克斯力，并得到了斯托克斯力的形式，但整个过程仍留有一个悬疑，即从微分几何理解应力张量，单位基矢和坐标基矢在球坐标系下，单位基矢表示为，```mathjax，\bfe，r=\frac，\bfr，r，\quad，\bfe，\theta=\frac，1，r，\frac，\pa...。

直播课程回顾在张朝阳的物理课第227期直播中，张朝阳回顾了使用微分几何求解非直角坐标系问题的便利性，并说明了梯度项的数学内涵，他应用微分几何计算了应力张量的第二项和第三对斯托克斯定律的贡献，单位基矢和坐标基矢在球坐标系下，单位基矢表示为，$$\mathbf，e，\alpha，=，\sin\theta\cos\phi，\sin\th...。