互联网神话的消退，网络效应和马太效应的局限导言互联网诞生之初，曾被誉为改变人类社会的革命性技术，随着时间的推移，一些曾经被深信不疑的互联网神话早已褪去光环，其中，网络效应和马太效应的局限性尤为值得我们深思，网络效应，一柄双刃剑网络效应是指随着用户数量的增加，产品的价值会呈指数级增长，梅特卡夫定律进一步指出，网络的价值与其节点数平方成正...。

数字化生存的神话与现实，互联网未带来世界大同导言互联网的兴起曾被视为人类社会的一场重大变革，预言着它将创造一个更加和谐、全球共识的世界，随着时间的推移，这些神话逐渐被现实所打破，网络效应的局限性网络效应被认为是互联网公司成功的铁律，即产品或服务的用户数量越多，其价值就越高，梅特卡夫定律更具体地指出，网络的价值与其节点数的平方成正比，实...。

自发热内衣冬季保暖服装市场上，很多贴身内衣标有自发热功能，号称服装自身可以发热为人体供暖，根据能量守恒定律，热量不能凭空产生，所有的自发热，实际都是借助外力发热，目前，市面上的自发热内衣，大部分是利用纤维吸湿发热的原理，也就是吸收了穿衣者自身的水分，来达到发热的功能，当纤维吸收水分时，纤维分子中的亲水基团与水分子结合，水分子的动能降低...。

随着冬季的到来，市面上各种保暖内衣层出不穷，号称可以抵御严寒，但在这些高科技加持的衣服背后，是真正的保暖还是智商税呢，自发热内衣，吸湿发热原理市场上许多保暖内衣宣称具有自发热功能，号称可以利用服装自身发热为人体供暖，但根据能量守恒定律，热量无法凭空产生，所谓的自发热，实际上是借助外力发热，目前市面上的自发热内衣，大部分是利用纤维吸湿发...。

自发热内衣冬天保暖服装市场上，许多贴身内衣标榜着自发热功能，号称服装本身可以发热为人体供暖，但是，根据能量守恒定律，热量不能凭空产生，所谓的自发热，实际上都是利用外力发热，市面上大多数的自发热内衣，是利用纤维吸湿发热的原理，也就是吸收穿衣者自身的水分，来达到发热的功能，当纤维吸收水分时，纤维分子中的亲水基团与水分子结合，水分子的动能降...。

保暖衣物黑科技，真保暖还是智商税，自发热内衣，无法凭空产热冬季保暖服装市场上，许多贴身内衣标榜自发热功能，声称服装可以自主发热为人体供暖，根据能量守恒定律，热量无法凭空产生，自发热内衣的原理其实在于纤维吸湿发热，即利用穿衣者的水分产生热能，北京石墨烯技术研究院院长王旭东博士表示，自发热的说法有些夸大，所有热量都需要热源，除非服装本身带...。

自发热内衣，原理揭秘冬季保暖服装市场上，许多贴身内衣标榜着自发热功能，号称可以自身发热为人体供暖，根据能量守恒定律，热量无法凭空产生，市面上的自发热内衣，大部分利用的是纤维吸湿发热的原理，即吸收穿衣者自身的水分，从而释放热量，当纤维吸收水分时，纤维分子中的亲水基团与水分子结合，水分子的动能降低，转换为热能释放出来，北京石墨烯技术研究院...。

纳维尔，斯托克斯方程是流体力学中描述流体运动的重要方程，它与牛顿运动定律有着密切的联系，牛顿运动定律描述作用在物体上的合力等于物体的质量与加速度的乘积，而纳维尔，斯托克斯方程描述作用在流体微元上的合力等于流体微元的质量与其加速度的乘积，以及来自流体粘度的力，矢量计算的张量化在传统的流体力学中，矢量微积分被用来进行矢量计算，使用张量语言...。

理解纳维尔，斯托克斯方程导言纳维尔，斯托克斯方程是流体力学中的一组基本方程，描述了流体的运动，这些方程源自牛顿运动定律，但表述方式不同，更适合流体动力学的分析，本文将从张量语言的角度介绍如何理解纳维尔，斯托克斯方程，并探讨其与牛顿运动定律之间的关系，张量语言在流体力学中的应用传统的流体力学教科书中，矢量微积分被用作数学工具，张量语言在...。

理解纳维尔，斯托克斯方程纳维尔，斯托克斯方程简介纳维尔，斯托克斯方程是一组非线性偏微分方程，描述了粘性牛顿流体的运动，它以法国物理学家克洛德，路易·纳维和爱尔兰物理学家乔治·加布里埃尔·斯托克斯的名字命名，纳维尔，斯托克斯方程与牛顿运动定律纳维尔，斯托克斯方程是牛顿第三定律在流体中的表达，牛顿第三定律指出，每个作用力都对应着一个大小相...。

前言在流体力学领域，纳维尔，斯托克斯方程是一组重要的偏微分方程，描述了流体的运动和行为，本篇文章将探讨如何理解纳维尔，斯托克斯方程，它与牛顿运动定律的关系，以及如何利用张量语言简化流体力学中的矢量计算，张量语言的优势在传统的矢量微积分中，流体力学中的计算往往复杂且繁琐，利用张量语言，我们可以显著简化这些计算，张量是描述物理量的多维数组...。

纳维尔，斯托克斯方程是流体力学中描述流体运动的基本方程，它描述了流体的速度、压力和温度随时间和空间的变化，该方程非常复杂，因此使用张量分析对其进行简化非常重要，牛顿运动定律与纳维尔，斯托克斯方程牛顿运动定律用于描述物体的运动，根据第三定律，作用在物体上的合力等于其质量与加速度的乘积，对于流体微元，作用在微元上的合力包括压力梯度和粘滞力...。

纳维尔，斯托克斯方程是流体力学中的一个基本方程，它描述了流体的运动，它是一个偏微分方程，通常简写为，```ρ，∂v，∂t，ρ，v⋅∇，v=，∇p，μ∇²v```其中，ρ是流体的密度v是流体速度p是流体的压力μ是流体的粘度```这个方程可以从牛顿第三定律推导出来，即作用力等于反作用力，考虑流体微元受到的力，根据牛顿第三定律，该力等于流...。

引言了解纳维尔，斯托克斯方程对于理解流体力学至关重要，而张量语言可以大大简化流体力学中的矢量计算，本文将探讨纳维尔，斯托克斯方程、牛顿运动定律和张量语言之间的关系，纳维尔，斯托克斯方程纳维尔，斯托克斯方程描述了流体的运动，是流体力学中的基本方程之一，该方程可以解释流体的粘性、密度和速度之间的关系，它等式右边的压强梯度项和粘滞项，恰好对...。

引言纳维尔，斯托克斯方程是流体力学中描述流体运动的基本方程组，它以牛顿第三定律为基础，表达了流体微元所受力的平衡关系，本文将从张量语言的角度出发，介绍如何理解纳维尔，斯托克斯方程，以及它与牛顿运动定律之间的关联，张量语言在流体力学中的应用张量语言是一种用于描述多维空间中矢量和二阶张量及其运算的数学工具，在流体力学中，张量语言可以极大地...。

纳维尔，斯托克斯方程是流体力学中的基本方程，描述了流体的运动，它是一个偏微分方程组，包含速度、压力和温度等流场变量，与牛顿运动定律的关系纳维尔，斯托克斯方程可以从牛顿第三定律推导而来，牛顿第三定律指出，作用在物体上的力等于物体对力的反作用力，对于流体微元，其受到的力包括压力梯度和粘滞力，张量语言在流体力学中的应用张量语言是一种数学工具...。

导言纳维尔，斯托克斯方程是流体力学中的基本方程，描述了流体的运动，它们以法国工程师克劳德，路易·纳维和英国数学家乔治·加布里埃尔·斯托克斯命名，与牛顿运动定律的关系纳维尔，斯托克斯方程是牛顿第三定律在流体中的表达，牛顿第三定律指出，作用在物体上的每一个作用力都对应着一个大小相等、方向相反的反作用力，在流体中，作用在流体微元上的作用力包...。

前言纳维尔，斯托克斯方程是流体力学的基础方程，它描述了流体的运动，理解这个方程可能会很具有挑战性，在文章中，我们将利用张量语言来简化流体力学中的矢量计算，并展示如何从牛顿运动定律导出纳维尔，斯托克斯方程，向量微积分到张量分析传统的流体力学依赖于向量微积分的数学工具，它涉及点乘、叉乘和复杂的导数运算，张量分析提供了一种更简洁的方法来处理...。

导言纳维尔，斯托克斯方程是流体力学中的一个关键方程，它描述了粘性流体的运动，理解这个方程对于理解各种流体现象，如湍流和边界层，至关重要，本文将介绍如何使用张量语言来简化纳维尔，斯托克斯方程的理解，并探讨其与牛顿运动定律之间的联系，矢量微积分和张量语言传统的流体力学使用矢量微积分来对流体运动进行描述，张量语言提供了一种更简洁和通用的方法...。

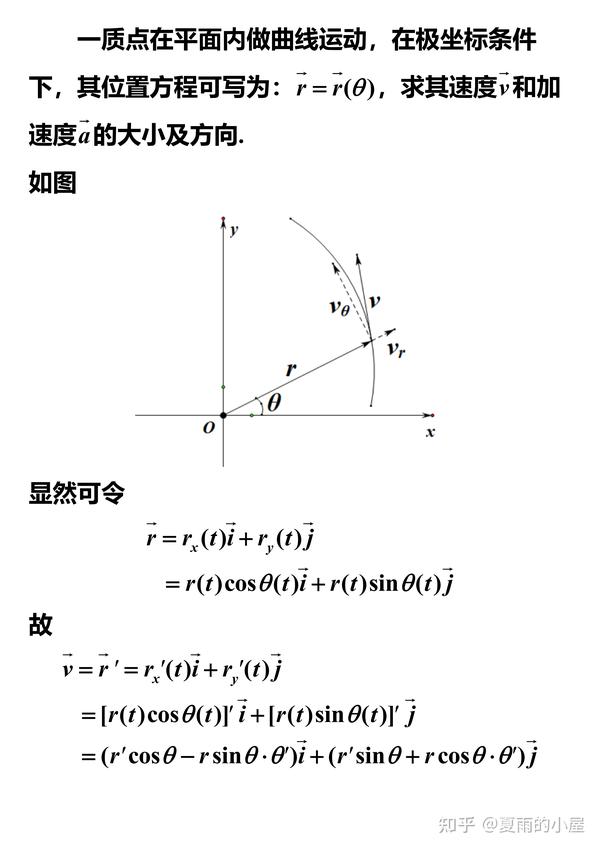
前言在前两期直播课中，我们使用微分几何的语言计算了斯托克斯力，并得出了斯托克斯力的形式，整个过程中仍留有一个悬念，即从微分几何的角度理解应力张量，本期直播课将彻底解决这一疑惑，回顾，非直角坐标系中的微分几何我们回顾了使用微分几何求解非直角坐标系问题的便利性，具体来说，单位基矢，球坐标系中，单位基矢表示为，```e，r=∂r，∂re，θ...。

sub>，∂inidS球坐标系中，法向导数∂ini为，∂ini=，∂êr，∂r，~=，1，r，êr因此，第三项可以写为，F3=，μ∫∫S，−pδij，μ，λ，Δij，μ∂jui，êj，1，r，êidS由于α=1，径向方向，，因此有，F3=，μ∫∫S，−pδ11，μ，λ，Δ11，μ∂1u1，1，r，dS计算出克氏符和度规分...。

课程回顾在上两节直播课中，张朝阳教授用微分几何的语言计算了斯托克斯力，并得到了斯托克斯力的形式，但在整个过程中，仍然留有一个悬念，即从微分几何理解应力张量，单位基矢和坐标基矢按照上一节直播课的数学符号精神，在球坐标系下，单位基矢表示为，e，r=，sin，phi，cos，theta，sin，phi，sin，theta，cos，phi...。

回顾上一节直播课中，张朝阳用微分几何的语言计算了斯托克斯力，并得到了斯托克斯力的形式，但整个过程仍留有一个悬疑，即从微分几何理解应力张量，单位基矢和坐标基矢在球坐标系下，单位基矢表示为，```mathjax，\bfe，r=\frac，\bfr，r，\quad，\bfe，\theta=\frac，1，r，\frac，\pa...。

纳维尔，斯托克斯方程是描述流体运动的基本方程组，它与牛顿运动定律紧密相关，本文将阐述如何利用张量语言简化流体力学中的矢量计算，从而更深入地理解纳维尔，斯托克斯方程，张量语言的引入传统的矢量微积分依赖于点乘和叉乘运算，而张量语言则提供了一种更简洁、更通用的方式来表示矢量和二阶张量等数学对象，矢量作为一阶张量，在张量分析中，矢量被视为一阶...。

直播课程回顾在张朝阳的物理课第227期直播中，张朝阳回顾了使用微分几何求解非直角坐标系问题的便利性，并说明了梯度项的数学内涵，他应用微分几何计算了应力张量的第二项和第三对斯托克斯定律的贡献，单位基矢和坐标基矢在球坐标系下，单位基矢表示为，$$\mathbf，e，\alpha，=，\sin\theta\cos\phi，\sin\th...。

纳维尔，斯托克斯方程概述纳维尔，斯托克斯方程是一组偏微分方程，描述了牛顿流体的运动，这些方程是流体力学的基础，用于预测和分析流体的行为，如湍流、粘性流动和边界层流动，纳维尔，斯托克斯方程的推导纳维尔，斯托克斯方程可以通过张量分析方法从流体应力张量中导出，流体应力张量描述了流体内部各点之间的力相互作用，利用牛顿第三定律，可以将流体微元的...。

与牛顿运动定律的关系纳维尔，斯托克斯方程是描述流体运动的微分方程组，它可以从牛顿运动定律导出，描述流体的运动如何受到压强梯度和粘滞力的影响，使用张量语言简化流体力学中的矢量计算张量语言是一种数学工具，它可以简化流体力学中涉及的矢量计算，张量可以表示为具有多个索引的量，这些索引表示张量的不同分量，使用张量语言，我们可以将流体应力张量中的...。

引言在上一节直播课中，张朝阳用微分几何的语言计算了斯托克斯力，并得到了斯托克斯力的形式，但是，整个过程中仍然存在一个疑问，即从微分几何的角度理解应力张量，本次直播课将彻底解决这个疑惑，微分几何基础单位基矢和坐标基矢在球坐标系下，单位基矢表示为$$\mathbf，\hat，e，r，=\sin\theta\cos\phi\mathbf，...。

纳维尔，斯托克斯方程是流体力学的基本方程，描述了流体运动的守恒定律，方程的矢量形式为，ρ，∂v，∂t，ρ，v·∇，v=，∇p，η∇²v其中，ρ是流体的密度v是流体的速度p是流体的压强η是流体的粘度等号左边的项表示流体的惯性，等号右边的项表示流体受到的力，包括压强梯度、粘滞力，纳维尔，斯托克斯方程与牛顿运动定律纳维尔，斯托克斯方程可以...。

作者，张雅婷编辑，杨锦新引言技术革命往往会催生出一批新的伟大公司和风云人物，AI狂奔两年多来，数不清的技术大佬加入了这场新浪潮，希望打造出下一个OpenAI，国内也涌现出了AI六小龙这样的明星初创企业，创业九死一生的定律在AI领域依旧生效，甚至头部效应比其他行业更加显著，融资集中，头部初创大获全胜有业内人士感叹道，头部初创拿钱到手软，...。